CALCULATION AND ANALYSIS OF TRANSFORMER INRUSH CURRENT BASED ON PARAMETERS
OF TRANSFORMER AND OPERATING CONDITIONS
Electrical and Electronics Project by Ravi Devani
Electrical and Electronics Project by Ravi Devani
INTRODUCTION
Magnetizing inrush current in transformers results from any abrupt changes
of the magnetizing voltage. This current in transformer may be caused by
energizing an unloaded transformer, occurrence of an external fault, voltage
recovery after clearing an external fault and out-of phase synchronizing of
connected generator. Because the amplitude of inrush current can be as high as
a short circuit current, a detailed analysis of the magnetizing inrush current
under various conditions is necessary for the concerns of a protective system
for the transformers. In this regard, some numerical and analytical methods
have been proposed in the literature. In analytical expressions for the magnetic
fluxes of no-load three-phase transformer is presented that can be used for
inrush current calculation. In by analytical solution of two differential equations
that governs the behavior of a transformer, the magnetic flux and inrush
current are determined. For modeling transformer core including hysteresis used
Jiles-Atherton theory and presented a new algorithm on a sample transformer. In
an analytic formula is presented to calculate the peak inrush current of a
nonlinear inductor with a series resistor. In a simple model for the transient
period of inrush current is presented. This model is developed from the
structural parameters of transformer. To avoid malfunction of protection system
under magnetizing inrush current, many researches are conducted for the
discrimination of inrush current from internal fault currents. For example, in
inrush current are discriminated from internal fault current by second harmonic
criterion. For discrimination of these currents used the sum of active power
flowing into the transformer from each terminal. In a criterion function in
terms of difference of amplitude of wavelet coefficients is defined. Then by
using this criterion function for three phases, the internal faults are discriminated
from the inrush current.
In this paper, first, the fundamentals of inrush current and the formulas
that are used for calculation it, are presented. Then a one-phase transformer
is simulated in
MATLAB and the effects of switching angle variation, energizing circuit
impedance and remnant flux on the characteristics of inrush current are
investigated in detail.
FUNDAMENTALS OF INRUSH CURRENT
It is very well known that a transformer will experience magnetizing inrush
current during energization. Inrush current occurs in a transformer whenever
the residual flux does not match the instantaneous value of the steady-state
flux which would normally be required for the particular point on the voltage
waveform at which the circuit is closed. For the explanation of the mechanism
causing inrush current in a transformer’s primary winding when connected to an
AC voltage source, we consider (1),
Where λ and v are the instantaneous flux in a transformer core and voltage drop
across the primary winding, respectively
v= dl/dt. (1)
As we see from (1), the rate of change of instantaneous flux in a
transformer core is proportional to the instantaneous voltage drop in the
primary winding or on the other hand, the flux waveform is the integral of the voltage
waveform. In continuously-operating transformer, these two waveforms are
shifted by 90°. But a significant difference exists between continuous-mode
operation and energization of a transformer. During continuous operation, the
flux level is at its negative peak when voltage is at its zero point, but
during energization the flux has to start at zero. So, for a rising voltage
just started from zero, the magnetic flux will reach approximately twice its normal
peak as it integrates the area under the voltage waveform’s first half-cycle.
This amount of flux, because of the nonlinear characteristic of the
magnetization curve, causes saturation of the transformer. During saturation, disproportionate
amounts of mmf are needed to generate magnetic flux. This means the winding
current, which creates the mmf to cause flux in the core, will disproportionately
rise to a value easily exceeding twice its normal peak. Fig. 1 shows the
generation of inrush current in a transformer. As seen from the figure,
exceeding flux from the knee point, results in large magnetizing current that
in some circumstances can be ten times of the rated current in a transformer.
Fig. 1. Generation of inrush current in a transformer
The general equation that gives the amplitude of inrush current as a
function of time can be expressed as (2):
Where Vm – maximum applied voltage; Zt – total impedance under inrush,
including system; φ – energization angle; t – time; t0 – point at which core saturates; τ – time constant of transformer
winding under inrush conditions; α – function of t0; Kw – accounts for 3 phase winding connection; Ks – accounts for short-circuit power of network.
For the purpose of designing a protective system for transformer, the peak
value of inrush current is an important factor. In these cases, a simplified
equation can be used to calculate the peak value of the first cycle of the inrush
current. This equation is as follow
Where Vm – maximum applied voltage; L – air core inductance of the
transformer; R – total dc resistance of the transformer; BN – normal rated flux density of
the transformer core; BR – remanent flux density of the transformer core; BS – saturation flux density of the core material.
As seen from the equations (2) and (3), the value of inrush current is
dependent to the parameters of transformer and operating conditions. So a
detailed analysis for finding the relations between the inrush current
characteristics and these factors are needed.
SIMULATION RESULTS
When a transformer is energized under no load or lightly loaded conditions,
inrush current may flow in the primary circuit. In this situation, the
equivalent circuit of transformer can be shown as Fig. 2 where Rs, Ls, Rp, Lm and
Rt are series resistance, series inductance, core losses resistance,
magnetizing inductance and source resistance respectively. In order to
investigate the effects of some parameters of transformer or network on the
inrush current of a typical transformer, a 120 VA, 60 Hz, (220/120) V
transformer with those parameters are presented in is selected. The parameters
of the equivalent circuit of this transformer referred to the 220V winding are
shown in Table 1.
Fig. 2. Equivalent circuit of the transformer under no
load
Table 1. Parameters of the simulated transformer
Also, the magnetization curve of the transformer is given in (4) where i
and λ are magnetizing current and flux respectively
i(l)=(63.084 x 10^-3) sinh(2.43l). (4)
It should be noted that equations are used to calculate the fundamental and
second harmonic components of inrush current, where N, T and f are number of samples in each cycle, period and frequency of the power
system, respectively. Also, m indicates fundamental and second components with
the numbers 1 and 2, respectively. The sampling rate of 30 kHz has been used in
this paper:
Electrical and Electronics Project by Ravi Devani
EFFECTS OF SWITCHING ANGLE
In this section, the effect of switching angle variation on the
characteristics of inrush current has been investigated. The remnant flux (Br) for all switching angles is 0.826 Wb-coil. Also the source resistance has
been considered to zero. Fig. 3 shows the effect of different switching angles
(θ) on the amplitude of inrush current. As seen from the figure, the highest
amplitude of inrush current is at 0° that is 5.52A. Also, it can be seen, increasing
of the switching angle will decrease the amplitude of inrush current.
Fig. 3. Effect of switching angle variation on the
amplitude of inrush current
The second harmonic content of inrush current is shown in Fig. 4. As seen
from this figure, increasing of the switching angle causes to a decrease in the
percentage second harmonic.
Fig. 4. Effect of switching angles in the percentage
second harmonic
It should be noted that, although, the highest amplitude of the inrush
current appears in the first cycle and then decays, but the highest percentage
second harmonic does not necessarily appear in the first cycle. For instance as
seen from Fig. 3 and Fig. 4, at θ=90°, both amplitude and
percentage second harmonic have been decreased with increasing cycle, but at θ=0°, although the amplitude of inrush current have been decreased, but second
harmonic firstly increased and then decreased. This is important when using
second harmonic content to restrain the relay operation during magnetizing
inrush conditions.
EFFECTS OF SOURCE RESISTANCE
In this case, the switching angle (θ) is 0°. Also, the remnant flux
(Br) is the same as the previous section. The effects of source resistance
have been considered by increasing Rt. Fig. 5 shows the effect of source
resistance on the amplitude of inrush current. As seen from figure, increasing
source resistance will decrease the amplitude of inrush current. Also, it
causes faster decay in the amplitude of inrush current. Therefore, it can be
said that transformers located closer to the generating plants display higher
amount of inrush currents lasting much longer than transformer installed
electrically away from generator.
Fig. 5. Effect of source resistance on the amplitude of
inrush current
The effect of source resistance in the percentage of second harmonic has
been shown in Fig. 6. The results show that the amount of percentage of second
harmonic will be decreased by increasing the source resistance.
Fig. 6. Effect of source resistance in the percentage
second harmonic
EFFECTS OF THE REMANENT FLUX
The effect of remnant flux on the first cycle peak current at different
switching angles is shown in Fig. 7. As seen from figure, the first cycle peak
current has large change when the remnant flux varies. Also the results indicate
that switching at θ=90° or Br=0 may not necessarily reduce the magnitude of inrush current. So, for reducing
inrush current, an appropriate switching angle by considering remnant flux must
be selected.
CONCLUSIONS
In this paper, the effects of some parameters on the characteristics of
inrush current are investigated in MATLAB Simulink.
Fig. 7. Effect of remnant flux on first cycle peak
current
Results show that increasing switching angle at a positive remnant flux or
source resistance will decrease the amplitude of inrush current. It has been
shown that largest second harmonic content may not necessarily appear at the
first cycle. The effect of remnant flux on the first cycle peak current shows
that it has large changes when the remnant flux varies. Also, it has been
concluded that for reducing inrush current, an appropriate switching angle by
considering remnant flux, must be selected.
REFERENCES
1. Blume L. F. Transformer Engineering. – New York: Wiley &
Sons, 1951.
2. Karsai K., Kerenyi D. and Kiss L. Large power transformers. – New
York: Elsevier, 1987.
3. L. Andriušienė, P. Kostrauskas, D. Mikalajūnas. Determination of
the Magnetic Fluxes of No–Load Three– Phase Power Transformer // Electronics
and Electrical Engineering. – Kaunas: Technologija, 2003. – No. 2(44). – P. 43–47.
4. Vanti M. G., Bertoli S. L. Semianalytic solution for a simple model
of inrush currents in transformers // IEEE Trans. Magnetics. – June, 2008. –
Vol. 44. – No.6. – P. 1270–1273.
5. Vahidi B., Tavakoli M. R. B. An algorithm for evaluating inrush
current in transformers using Jiles–Atherton theory of ferromagnetic hysteresis
// IEEE Conf. Tencon, Hong Kong. – November, 2006. – P. 1–4.
6. Wang Y., Abdulsalam S. G., Xu W. Analytical formula to estimate
the maximum inrush current // IEEE Trans. Power Delivery. – April, 2008. – Vol.
23. – No. 2. – P. 1266–1268.
7. Chen S. D., Lin R. L. Magnetizing inrush model of transformers
based on structure parameters // IEEE Trans. Power Delivery. – July, 2005. –
Vol. 20. – No.3. – P. 1947–1954.
8. Sykes J. A., Morrison I. F. A proposed method of harmonic restraint
differential protecting of transformers by digital computer // IEEE Trans.
Power App. Systems. – May, 1972. – Vol. PAS–91. – No. 3. – P. 1266–1272.
9. Kasztenny B., Kulidjian A. An improved transformer inrush restraint
algorithm increases security while maintaining fault response performance //
53rd Annual Conference for Protective Relay Engineers. – April, 2000. –P. 1–27.
10. Wang J. Hamilton R. Analysis of transformer inrush current and
comparison of harmonic restraint methods in transformers protection // 61st
Annual Conference for Protective Relay Engineers. – April, 2008. – P. 142–169.
11. Yabe K. Power differential method for discrimination between
fault and magnetizing inrush current in transformers // IEEE Trans. Power
Delivery. – July, 1997. – Vol. 12. – No.3. – P. 1109–1118.
12. Faiz J. Lotfi–Fard S. A novel wavelet–based algorithm for discrimination
of internal faults from magnetizing inrush currents in power transformers //
IEEE Trans. Power Delivery. – October, 2006. – Vol. 21. – No. 4. – P. 1989–
1996.
13. Sonnemann W. K., Wagner C. L., Rockefeller G. D. Magnetizing Inrush
Phenomena in Transformer Banks // AIEE Transaction. – October, 1958. – Part
III. – Vol. 77. – P. 884–892.
Electrical and Electronics Project by Ravi Devani


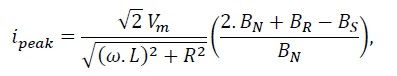








No comments:
Post a Comment