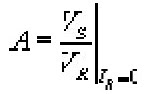DIRECT TORQUE CONTROL OF BLDC MOTOR USING FUZZY LOGIC IN LABVIEW

DIRECT TORQUE CONTROL OF BLDC MOTOR USING FUZZY LOGIC IN LABVIEW

ABSTRACT

Brushless dc motors are widely used in many industrial applications due to their high efficiency, high power density and ease of control. In this paper, sensorless direct torque control (DTC) of bldc motor is implemented using fuzzy logic. In actual DTC both torque and stator flux linkage is controlled. In the proposed system, the control of stator flux linkage is avoided because every commutation will cause the stator flux linkage decreasing dramatically and sharp dip appears on the locus of the stator flux linkage every 60 electrical degrees. The best way to control the stator flux linkage amplitude is to know the exact shape of it, but it is considered too cumbersome in the constant torque region. Therefore the amplitude of stator flux linkage can be considered as a constant. The proper voltage vector selection is done using fuzzy logic controller which improves the dynamic performance. The sensorless operation is achieved by using a state observer. All the simulations were done in LabVIEW software of virtual instrumentation.

Keywords—Brushless DC motor(BLDC), Direct torque control (DTC), fuzzy Logic controller, stator flux linkage, voltage vector selection, state observer, LabVIEW, virtual instrumentation.

INTRODUCTION

Permanent magnet Brushless DC (BLDC) motors are nowadays widely used in industries such as HVAC industry, medical, electric traction, road vehicles, aircrafts, military equipment, hard disk drive, etc. due to their high efficiency, high power density, reliability and ease of control. Today there are basically two types of instantaneous electromagnetic torque controlled ac drives used for high-performance applications: vector and direct torque control (DTC) drives. The vector control, the most popular method uses a decoupling control which transforms the motor equations into a coordinate system that rotates in synchronism with the rotor flux vector. The second method, Direct Torque Control (DTC) is a form of hysteresis or bang-bang control to control torque (and thus speed) of electric motors. The basic concept behind the DTC of ac drive, as its name implies, is to control the electromagnetic torque and flux linkage directly and independently by the use of six or eight voltage space vectors found in lookup tables. The advantages associated with DTC are simplicity and high dynamic performance, no vector transformation and faster torque response. The torque ripple is the major problem associated with DTC (1-8).Various papers proposed new methods for eliminating the problems associated with classical DTC. Some papers proposed multilevel inverter in which there are more voltage space vectors available to control the flux and torque and hence smoother torque can be obtained

(2). Here more power switches are required which increases system cost and complexity. In (6) and (11) two PI regulators are required to control the flux and torque and they need to be tuned properly. In DTC,\ the stator flux is estimated by integrating the back- EMF which should be reset regularly to reduce the effect of the dc offset error. In papers (12), (13) dc offset is eliminated by introducing low pass filters for estimating the stator flux linkage. In this paper fuzzy logic is used for proper voltage vector selection. Fuzzy logic can be considered as a mathematical theory combining multi-valued logic, probability theory, and artificial intelligence to simulate the human approach in the solution of various problems by using an approximate reasoning to relate different data sets and to make decisions. It has been reported that fuzzy controllers are more robust to plant parameter changes than classical PI or controllers and have better noise rejection capabilities. The introduction of fuzzy logic quickens the torque response and provides smooth torque. Hence overall static and dynamic performance can be improved (7- 8).The torque and rotor speed are obtained from the back-EMFs, which are estimated using a state observer. In this paper, all simulations had done in the LabVIEW (Laboratory Virtual Instrument Engineering Workbench) software. In comparison with the other software tools, the simulation with LabVIEW provides easy debugging features and user friendly environment. The conventional six step control of BLDC motor is also simulated. The simulation results shows that the proposed DTC scheme using fuzzy logic has good control performance, compared with conventional method.

BLDC MOTOR DRIVE MODEL

The assumptions made for modeling BLDC motor are

1) The motor’s stator is a star wound type.

2) The motor’s three phases are symmetric, including their resistance, inductance and mutual inductances.

3) There is no change in rotor reluctance with angle due to non-salient rotor.

The BLDC motor is modeled in the stationary reference frame using phase currents, speed, and rotor position as state variables. The BLDC motor is modeled as

(1)

Where Va,Vb,Vc, Ia,Ib,Ic, and Ea,Eb,Ec are the stator voltages, stator currents and back-EMFs of all the three phases respectively, R and L are the resistance and inductance of stator phase winding respectively and p is the differential operator(d/dt).

The generated electromagnetic torque is given by

(2)

where ω is the speed.

The induced back-EMFsis of trapezoidal shapes and can be written as

Ea = fa(θ)λω (3)

Eb = fb(θ)λω (4)

Ec = fc(θ)λω (5)

wherefa(θ), fb(θ), fc(θ) are functions having trapezoidal shapes as back-EMFs and λ is the back-EMF constant.

BLDC – DTC SYSTEM

A conventional six-switch 3-phase inverter fed BLDC motor in two-phase conduction mode, as show in Fig. 1.

Fig. 1. An inverter driving BLDC motor

The primary voltages Van, Vbn, and Vcn are determined by the status of the six switches, S1, S2, S3, S4, S5 and S6. There are six nonzero voltage vectors:- V1(100001), V2(001001), V3(011000), V4(010010),V5(000110), V6(100100) and one zero voltage vector V0(000000). The six nonzero voltage vectors are 60 degrees apart from each other as in Fig. 2.

Fig. 2. Stator flux linkage space vector representation

The basic principle of direct torque control (DTC) is to choose the appropriate stator voltage vector out of eight possible voltage vectors according to the difference between the reference and actual torque and flux linkage so that the stator flux linkage vector rotates along the stator reference frame trajectory and produces the desired torque. The stator flux is controlled by properly selecting voltage vectors and hence the torques by stator fluxes rotation. The faster torque response is achieved by increasing the stator vector rotation speed. In this proposed paper (14), the DTC of a BLDC motor drive operating in two-phase conduction mode is simplified by controlling only torque and by intentionally keeping the stator flux linkage amplitude constant by eliminating the flux control in the constant torque region. Since the flux control is removed, fewer algorithms are required for the proposed control scheme. There is no need to control the stator flux linkage amplitude of a BLDC motor in the constant torque region due to the sharp changes which occur every 60 electrical degrees and hence the flux control is quite difficult. Therefore the stator flux linkage amplitude is kept almost constant on purpose and only torque is controlled. Also the zero voltage vector suggested in to decrease the electromagnetic torque could have some disadvantages, such as generating more frequent and larger spikes on the phase voltages that deteriorate the trajectory of the stator flux-linkage locus, increase the switching losses, and contributes to the large common-mode voltages that can potentially damage the motor bearings. To overcome these problems, a new simple voltage space vector look-up table is developed. The rotating speed of the stator flux linkage can be controlled easily by selecting proper voltage vector. For instance, in the region I of Fig. 2, for counterclockwise operation, if the actual torque is bigger than the reference, voltage vector V5 is selected to keep flux linkage rotating in the reverse direction. The torque angle decrease as fast as it can, and the actual torque decrease as well. Once the actual torque is smaller than the reference, voltage vector V2 is selected to increase torque angle and the actual torque. Hence the region of the stator flux linkage is known, selecting proper voltage vector can reach fast torque

control. The new simplified switching table is as follows:

TABLE I

THE SWITCHING TABLE FOR INVERTER

Here the ET represents the error in torque and is determined by the difference between reference torque and estimated torque. The value ‘0’ or ‘1’ stands for that the estimated value is smaller or bigger than the reference value respectively. I, II, III…, VI denotes the stator flux linkage region.

BLDC-DTC SYSTEM USING FUZZY LOGIC

In the past decade, fuzzy logic control techniques have gained much interest in many applications. Fuzzy Logic is a form of many-valued logic or probabilistic logic. It deals with reasoning that is approximate rather than fixed and exact. In traditional logic theory, have two valued logic-true or false (0 or 1). It has been extended to handle the concept of partial truth, where the truth value may range between completely true and completely false. They have a real time basis as a human type operator, which makes decision on its own basis. In the proposed BLDC-DTC system the fuzzy logic controller is used for selecting the proper voltage vector. It involves basically three steps:-

A. Fuzzification

The fuzzification is the process of a mapping from input to the corresponding fuzzy set in the input universe of discourse. There are two inputs to the fuzzy logic controller: - Torque error (ET) and angle information. Output of the fuzzy logic controller is proper voltage vector (V1 to V6).Torque error (ET) is divided into four fuzzy subsets with the linguistic value {PB, PS, NS, NB} and its universe of discourse is [-0.1 0.1]. Flux linkage angle (Angle) is divided into six fuzzy subsets {A1, A2, A3, A4, A5, A6} and its universe of discourse is [-π π]. The output Space voltage vector (V) is divided into six singleton fuzzy subsets {V1, V2, V3, V4, V5, V6}. Membership functions of twofuzzy input variables (ET and Angle) and one fuzzy output variables (Vi) are triangle type as shown in Fig.3.

(a) Membership function of torque error

(b) Membership function of flux linkage angle

(c) Membership function of space voltage vector

Fig. 3. Membership functions of the fuzzy controller

B. Rules and fuzzy reasoning

Fuzzy control rules are expressed in the IF-THEN format as IF ET is Ai and Angle is Bi, THEN V is Vi Where Ai, Bi, Vi denote fuzzy sets. The entire fuzzy rules expressed as a table as shown in the table II

TABLE II

FUZZY REASONING RULES FOR BLDC- DTC

Mamdani’s Min-Max method is employed in the fuzzy reasoning.

C. Defuzzification

The defuzzification is not required in the controller because output of the fuzzy controller is just six singleton fuzzy subsets which are the actual PWM voltage vector sequence composed of only seven different states, and these states could be directly used as the successor of the fuzzy rules.

SENSORLESS OPERATION USING BACK-EMF OBSERVER

In BLDC motor, the electromagnetic torque can be estimated directly from the back-EMF and the speed.

Here in this proposed method, an observer is used to estimate the back-EMF waveform. By choosing α- axis and β-axis stator currents and back-EMFs as the state-variables, the following state equations can be obtained

ẋ = Ax + Bu(6)

y = Cx(7)

Where x = [ia, ib, ea, eb]T is the state vector, u = [ua, ub]T is the input vector, y = [ia, ib]T is the output vector, and

The back-emf is estimated as

e^= K (y -y^)(8)

Where e^ = [ea, eb]T is the back-EMF vector, K= diag(k1, k2) is the gain matrix, k1 and k2 are positive constants. The relation between the rotor speed and amplitude of the back-EMF is given by

E = PKeω(9)

Where P is the number of pole pairs, Ke is the back- EMF constant of the motor, E is the amplitude of every phase back- EMF. The estimated speed is given by

The estimated rotor position is obtained by θ􀷠

 

LabVIEW IN VIRTUAL INSTRUMENTATION

LabVIEW (Laboratory Virtual Instrumentation Engineering Workbench) is a graphical programming language that uses icons instead of lines of text to create applications.LabVIEW programs are called virtual instruments, or Vis, because their appearance and operation imitate physical instruments, such as oscilloscopes and millimeters. Every VI uses functions that manipulate input from the user interface or other sources and display that information or move it to other files or other computers. LabVIEW object oriented programming uses concepts from other object oriented programming languages such as C++ and Java, including class, structure, encapsulation, and inheritance. We can use these concepts to create code that is easier to maintain and modify without affecting other sections of code within the application. We can use object oriented programming in LabVIEW to create user-defined data types. That is different types of physically existing systems can be simulated using this software. Here in this project we are using this software to design the control schemes of hybrid electric vehicle. The advantage of the LabVIEW software over other simulating software is that a wide range of hardware components are available which are helpful in testing as well as implementation of various applications that we develop in this software. In this proposed paper all the simulations had done in LabVIEW software.

BLOCK DIAGRAM OF SENSORLESS FUZZY BLDC-DTC SYSTEM

The block diagram of a sensorless fuzzy based BLDC DTC system is shown in Fig. 4. In the proposed system, there is an inner torque loop and outer speed loop. The reference torque is obtained from the speed controller and is limited at a certain value. Both voltages and currents are measured and then transformed into the stationary reference frame alphabeta components in the system.A back-EMF observer provides the estimated back-EMF. A fuzzy logic controller generates the switching signal which drives the inverter.

Fig. 4. Block diagram of proposed fuzzy BLDC-DTC system

SIMULATION RESULTS

All the simulations had done in LabVIEW software.The parameters of the BLDC used in the system are listed in the table 3.

TABLE III

BLDC MOTOR SIMULATION PARAMETERS

Fig. 6 shows the performance comparison between the conventional PWM method using the sensor and the proposed method. The torque ripple and the current ripple are much less, compared with the PWM scheme. A load torque of 2 Nm is applied. The figure shows the response performance of the proposed sensorless drive at 1000 rpm. Although the small deviation occurred after injecting the load, the performance is generally good.

(a) Theta waveform

(b) Current waveform

(c) Actual speed response for a reference speed of 1000 rpm

(d) Electromagnetic torque for a load torque of 2 Nm

Fig. 5. Simulation results of the proposed fuzzy based DTC scheme

(e) Actual speed response for a reference speed of 1000 rpm

(f) Electromagnetic torque for a load torque of 2 Nm

Fig. 6. Simulation results of conventional PWM method

CONCLUSION

The proposed two-phase conduction mode for DTC of BLDC motors is introduced as opposed to the conventional PWM control in the constant torque region. Much faster torque response is achieved compared to conventional PWM current and especially voltage control techniques. It is also shown that in the constant torque region under the two-phase conduction DTC scheme, the amplitude of the stator flux linkage cannot easily be controlled due to the sharp changes and hence it is kept constant. The proper voltage vector selection is done using fuzzy logic controller which improves the dynamic performance. The sensor less operation is achieved by using a state observer which also improves the performance. Fuzzy controller is virtually created in LabVIEW and utilized to implement the algorithm.

Speed control of BLDC motor is achieved using virtual instrumentation. This proposed method controls the speed for various ranges. The simulation results show that the proposed scheme has good estimation performance in low and high speed range and good control performance, compared with the conventional PWM method.

REFERENCES

[1] Y. Liu, Z. Q. Zhu, D. Howe, ”Direct torque control of brushless DCdrives with reduced torque ripple,” IEEE Trans. Ind. Appl., vol. 41, no.2, pp. 599-608, 2005.

[2] L. Zhong, M. F. Rahman, W. Y. Hu, K. W. Lim, ”Analysis of DirectTorque Control in Permanent Magnet Synchronous Motor Drivers,” IEEETrans. on Power Electronics, vol. 12, no. 3, pp. 528-535, 1997.

[3] Won Chang-hee, Song Joong-Ho,lck Choy, ”Commutation torque ripplereduction in brushless DC motor drives using a single DC current sensor,” Power Electronics, IEEE Transactions on, vol. 19, no. 2, pp, 312-319, 2004.

[4] S. J. Kang, S. K. Sul, ”Direct torque control of brushless DC motorwithnon-ideal trapezoidal back-EMF,” IEEE Trans. Power Electron., vol. 10, no. 6, pp. 796-802, 1995.

[5] S. K. Chung, H. S. Kim, C. G. Kim, and M. J. Youn, “A new instantaneoustorque control of PM synchronous motor for high-performance direct-drive applications,” IEEE Trans. Power Electron., vol. 13, no. 3, pp. 388–400, May 1998.

[6] M. Ehsani, R. C. Becerra, ”High-speed torque control of brushlesspermanent magnet motors,” IEEE Trans. Ind. Electron.. vol. 35, no. 3, pp. 402-406, 1988.

[7] Do Wan Kim, Ho Jae Lee, and Masayoshi Tomizuka, “FuzzyStabilization of Nonlinear Systems under Sampled- Data Feedback: An Exact Discrete-Time Model Approach,” IEEE Transactions on Fuzzy Systems, Vol. 18, No. 2, Apr.

2010, pp: 251 – 260.

[8] Zdenko Kovaccic and Stjepan Bogdan, “Fuzzy Controller designTheory and Applications”, © 2006 by Taylor & Francis Group. international, 2002.

[9] D. Grenier, L. A. Dessaint, O. Akhrif, J. P. Louis, “A parklike transformationfor the study and the control of a nonsinusoidal brushless dc motor,” in Proc. IEEE-IECON Annu. Meeting, Orlando, FL, Nov. 6-10, 1995, vol. 2, pp.

836–843.

[10] K. Y. Cho, J. D. Bae, S. K. Chung, and M. J. Youn, “Torque harmonicsminimization in permanent magnet synchronous motor with back-EMF estimation,” in Proc IEE Elec. Power Appl., vol. 141, no. 6, pp. 323–330, 1994.

[11] C. Lascu, I. Boldea, and F. Blaabjerg, “A modified direct torque control forinduction motor sensorless drive,” IEEE Trans. Ind. Appl., vol. 36, pp. 122–130, Jan./Feb. 2000.

[12] B. K. B. And and N. R. Patel, “A programmable cascaded low-pass filter-basedflux synthesis for a stator flux-oriented vector-controlled induction motor drive,” IEEE Trans. Ind. Electron., vol. 44, pp. 140–143, Feb. 1997.

[13] M. F. Rahman, Md. E. Haque, L. Tang, and L. Zhong, “Problems associated withthe direct torque control of an interior permanent-magnet synchronous motor drive and their remedies,” IEEE Trans. Ind. Electron., vol. 51, pp. 799–809, Aug. 2004.

[14] Y. Liu, Z. Q. Zhu, and D. Howe, “Direct torque control of brushless dc driveswith reduced torque ripple,” IEEE Trans. Ind. Appl., vol. 41, no. 2, pp. 599–608, Mar./Apr. 2005.

[15] W. S. H. Wong, D. Holliday, “Constant inverter switching frequency directtorque control,” in Proc. IEE-PEMD Annu. Meeting, Bath, UK, Jun. 4-7, 2002, pp. 104–109.

SIMULATION OF EXTRA HIGH VOLTAGE LONG TRANSMISSION LINES

SIMULATION OF EXTRA HIGH VOLTAGE LONG TRANSMISSION LINES

ABSTRACT

The electrical power system mainly consists of three principle divisions the generating stations, y he transmission system and the distribution system. The transmission lines are the connecting links between generating station and the distribution system and lead to other power system interconnections. Now a day, we are using Extra High Voltage (EHV) transmission lines for transmission of power between the generating station and distribution system .The main reasons behind it are the construction of super power stations of very large capacities necessities the transmission at high voltage for this we use EHV lines.At high voltages power loss is also reduced because losses are directly proportional to the square of current. The simulation of transmission line using MATLAB helps us to analyze the behaviors and parameters of transmission line under actual conditions. We are simulating a long transmission line and analyze the waveforms at sending and receiving end. The results obtained after simulation are used in the designing of Extra High Voltage Long Transmission Line Model.

INTRODUCTION

Electrical energy is generated in large hydro electric, thermal and nuclear super and super critical power stations these stations are generally situated far away from the load centers. This necessitates an extensive power supply network between the generating station and consumer load. This network may be divided into two parts transmission and distribution the main part of this transmission system. Transmission line transmits bulk electrical power from sending end to receiving end stations without supplying any consumer en route and it can be divided into two parts primary and secondary. The transmission voltage is re 66kV, 110kV, 132kV, 220kV, 400kV and 765kV.

The more the voltages of transmission line the better the performance and efficiency of the system. For this we use high voltage and extra high voltage transmission lines to transmit electrical power from the sending end substations to the receiving end substations. At the receiving end substations the voltage is stepped down to a lower value of 66kV, 33kv or 11kV. The secondary transmission system forms the link between the main receiving end substations and secondary substations. In the transmission line the voltage can vary as much as 10% or even 15% DUE TO variation in loads the transmission line is the main energy corridor in a power system. The performance of a power system is mainly dependent on the performance of the transmission lines in the system. It is necessary to calculate the voltage current and power at any point on the transmission line provided the values at one point are known. We are aware that in 3 phase circuit problem it is sufficient to compute results in one phase and subsequently predict results in the other 2 phases by exploiting the three phase symmetry. Although the lines are not spaces equilaterally and not transposed the resulting asymmetry is slight and the phases are considered to be balanced as such transmission line calculations are also carried out on per phase basis.

The transmission line performance is governed by its four parameters

Series resistance

Series inductance

Shunt capacitance

Shunt conductance

All these parameters are distributed over the length of the line. The insulation of a line us seldom perfect and leakage currents flow over the surface of insulators especially during bad weather this leakage is simulated by shunt conductance. The shunt conductance is in parallel with the system capacitance. Generally the leakage currents are small and the shunt conductance is ignored in calculations.

The transmission line may be classified as short, medium and long. When the length of the line is less than about 80km the effect of shunt capacitance can be ignored and the line is designated as a short line. When the length is between 80 and 250km the shunt capacitance can be considered as lumped and the line is termed as medium length line. Lines more than 250km long require calculation in terms of distributed parameters are knows as ling lines.

Two Port Networks

A pair of terminals at which a signal (voltage or current) may enter or leave is called a port. A network having only one such pair of terminals is called a one port network.

 

Figure 1. Two-port network

A two-port network (or four-terminal network, or quadripole) is an electrical circuit or device with two pairs of terminals. Examples include transistors, filters and matching networks. The analysis of two-port networks was pioneered in the 1920s by Franz Breisig, a German mathematician.

A two-port network basically consists in isolating either a complete circuit or part of it and finding its characteristic parameters. Once this is done, the isolated part of the circuit becomes a "black box" with a set of distinctive properties, enabling us to abstract away its specific physical buildup, thus simplifying analysis. Any circuit can be transformed into a two-port network provided that it does not contain an independent source.

A two-port network is represented by four external variables: voltage and current at the input port, and voltage and current at the output port, so that the two-port network can be treated as a black box modeled by the relationships between the four variables Vs, Is, Vr and Ir. There exist six different ways to describe the relationships between these variables, depending on which two of the four variables are given, while the other two can always be derived.

Note: All voltages and currents below are complex variables and represented by phasors containing both magnitude and phase angle.

The parameters used in order to describe a two-port network are the following: Z, Y, A, h and g. They are usually expressed in matrix notation and they establish relations between the following parameters:

(1)Input voltage V1

(2) Output voltage V2

(3) Input current I1

(4) Output current I2

ABCD Parameters

 

Figure 2.transmission network

Two port representation of a transmission network.

Consider the power system shown above. In this the sending and receiving end voltages are denoted by VS and VR respectively. Also the currents IS and IR are entering and leaving the network respectively. The sending end voltage and current are then defined in terms of the ABCD parameters as

So,

This implies that A is the ratio of sending end voltage to the open circuit receiving end voltage. This quantity is dimension less. Similarly,

 

i.e., B , given in Ohm, is the ratio of sending end voltage and short circuit receiving end current. In a similar way we can also define

 

Also,

The parameter D is dimension less.

Note: Here A and D are dimensionless coefficients, B is impedance andC is admittance. A negative sign is added to the output current I2in the model, so that the direction of the current is out-ward, for easy analysis of a cascade of multiple network models.

SIMULATION

Various blocks used

Resistor

The Resistor block models a linear resistor, described with the following equation:

Where,

V Voltage

I Current

R Resistance

Connections + and – are conserving electrical ports corresponding to the positive and negative terminals of the resistor, respectively. By convention, the voltage across the resistor is given by V(+) – V(–), and the sign of the current is positive when flowing through the device from the positive to the negative terminal. This convention ensures that the power absorbed by a resistor is always positive.

Capacitor

The Capacitor block models a linear capacitor, described with the following equation:

Where,

I Current

V Voltage

C Capacitance

t Time

Inductor

The Inductor block models a linear inductor, described with the following equation:

Where,

I Current

V Voltage

L Inductance

t Time

Voltage Sensor

The Voltage Sensor block represents an ideal voltage sensor, that is, a device that converts voltage measured between two points of an electrical circuit into a physical signal proportional to the voltage.

Voltage Measurement

The Voltage Measurement block measures the instantaneous voltage between two electric nodes. The output provides a Simulink signal that can be used by other Simulink blocks.

AC Voltage Source

The AC Voltage Source block implements an ideal AC voltage source. The generated voltage is described by the following relationship:

Negative values are allowed for amplitude and phase. A frequency of 0 and phase equal to 90 degrees specify a DC voltage source. Negative frequency is not allowed; otherwise the software signals an error, and the block displays a question mark in the block icon.

Scope

The Scope block displays its input with respect to simulation time.

The Scope block can have multiple axes (one per port) and all axes have a common time range with independent y-axes. The Scope block allows you to adjust the amount of time and the range of input values displayed. You can move and resize the Scope window and you can modify the Scope's parameter values during the simulation.

Solver Configuration

Each physical device represented by a connected Simscap block diagram requires global environment information for simulation. The Solver Configuration block specifies this global information and provides parameters for the solver that your model needs before you can begin simulation.

Each topologically distinct Simscape block diagram requires exactly one Solver Configuration block to be connected to it.

Breaker

The Breaker block implements a circuit breaker where the opening and closing times can be controlled either from an external Simulink signal (external control mode), or from an internal control timer (internal control mode).

Ground

The Ground block implements a connection to the ground.

Add

The Add block performs addition or subtraction on its inputs. This block can add or subtract scalar, vector, or matrix inputs. It can also collapse the elements of a signal.

Sine Wave

The Sine Wave block provides a sinusoid. The block can operate in either time-based or sample-based mode.

Fcn Block

The Fcn block applies the specified mathematical expression to its input. The expression can be made up of one or more of these components:

• u - The input to the block. If u is a vector, u(i) represents the ith element of the vector; u(1) or u alone represents the first element.
• numeric constants
• Arithmetic operators (+ - * /^)
• Relational operators (== != ><>= <=) — The expression returns 1 if the relation is true; otherwise, it returns 0.
• Logical operators (&& || !)-The expression returns 1 if the relation is true; otherwise, it returns 0.
• Parentheses
• Mathematical functions — abs, cos, sin, exp, log, pow, tan, sinh, sqrt etc.
• Workspace variables — Variable names that are not recognized in the preceding list of items are passed to MATLAB for evaluation.

PI Section Line

The PI Section Line block implements a single-phase transmission line with parameters lumped in PI sections. For a transmission line, the resistance, inductance, and capacitance are uniformly distributed along the line. An approximate model of the distributed parameter line is obtained by cascading several identical PI sections, as shown in the following figure.

Unlike the Distributed Parameter Line block, which has an infinite number of states, the PI section linear model has a finite number of states that permit you to compute a linear state-space model. The number of sections to be used depends on the frequency range to be represented.

PS Simulink Converter

The PS-Simulink Converter block converts a physical signal into a Simulink output signal. Use this block to connect outputs of a Physical Network diagram to Simulink scopes or other Simulink blocks.

The Output signal unit parameter lets you specify the desired units for the output signal. These units must be commensurate with the units of the input physical signal coming into the block. The Simulink output signal is unitless, but if you specify a desired output unit, the block applies a gain equal to the conversion factor before outputting the Simulink signal. For example, if the input physical signal coming into the block is displacement, in meters, and you set Output signal unit to mm, the block multiplies the value of the input signal by 10e3 before outputting it.

Display

The Display block shows the value of its input on its icon. You control the display format using the Format parameter:

• short - displays a 5-digit scaled value with fixed decimal point
• long - displays a 15-digit scaled value with fixed decimal point
• short_e - displays a 5-digit value with a floating decimal point
• long_e - displays a 16-digit value with a floating decimal point
• bank - displays a value in fixed dollars and cents format (but with no $ or commas)
• hex (Stored Integer) - displays the stored integer value of a fixed-point input in hexadecimal format
• binary (Stored Integer) - displays the stored integer value of a fixed-point input in binary format
• decimal (Stored Integer) - displays the stored integer value of a fixed-point input in decimal format
• octal (Stored Integer) - displays the stored integer value of a fixed-point input in octal format

First Simulation Model

In this we tried to implement the simulation of the transmission line by using its equivalent diagram.

 

Figure 3.first simulation model

Although there were no errors but the simulation was not showing desired results. There was also no consideration of length and solver configuration block was not implemented correctly.

Second Simulation Model

Consider the standard model1 of a transmission line (Fig. 4).

 

Figure 4. standard model of transmission line

Both the voltages and the currents can be separately analyzed using Kirchhoff‘s laws and put in terms that can be analyzed using Simulink. Let’s analyze the model, writing all time-based variable sin the transmission line in terms of the Laplace transform variable, s. The spatial variation of the transmission line will be in corporated into the discrete section number:

For the simulation of the voltage response of the transmission line, the voltageV1 across the capacitor in the first loop (which includes the voltage source in Fig.4) can be written in terms of the voltage source, Vs, and the voltage in the second loop V2 as

(1) 

Where, Zsis the source impedance. In the transmission line, the elements L and C are the inductance per unit length, and the capacitance per unit length, respectively. The voltage across the capacitor in an Intermediate loop, n, can be written in terms of the similar voltage Vn-1 in the previous loop (n-l), and the voltage Vn+1 in the following loop (n+1).

(2)

A load impedance, ZL, is in parallel with the capacitor in the final loop, k. The load impedance can be linear or nonlinear.

We define the current in the load impedance at the end node, k, via the relation

(3)

Where g( Vk) is an arbitrary nonlinear function that has to be specified by the simulator. In the linear case, g(Vk) is equal to a constant multiplied by V(Fig. 5). From Fig. 5, we find the voltage Vk to be

(4)

 

Figure 5.simulink simulation of the voltage response of the transmission line

For purposes of simulating the current response of the transmission line, the current in the first loop (which includes the voltage source in Fig. 4) can be written in terms of the voltage source V, and the current in the second loop i2.

(5)

The current in an intermediate loop, n can be written in terms of the current in the previous loop (n-1) and the following loop (n+1):

(6)

For the case of linear load impedance, i =V/ZL, the load impedance ZL is in parallel with the capacitor in the final loop, k. The current in this loop is written in terms of the current in the previous loop (k-1)

(7)

Equations 5-7 determine the elements of a second transmission line. In Fig, 5, the critical Simulink elements are shown for the elements specified with Equations 1-4. A dialog menu with Simulink allows all parameters of the polynomial to be specified. We specify the voltage source, Vs, as a half sine wave generator, which acts as a pulse generator in the simulation. The amplitude and width were controllable parameters. In our application, fifteen identical intermediate elements were used. Although we will use only a Limited number of sections in our transmission line model, it can be generalized to include as many as desired.

In addition, the user can specify numerical values for the circuit elements L, C, Zs, and ZL. For clarity of presentation, we include as equentially increasing “dc offset” to each section. Both linear [ik=g(Vk) = constant*Vk] and nonlinear [ik=g(Vk)] load impedancesare described with this model.

 

Figure 6.matlab simulation model

MATLAB simulation model

But there were two major problems that we were unable to solve First of all there was no reference to the length of line.

Second the type of function to be used was unknown.

Third Simulation Model

In this we have used a PI Section Line and specifies all the required parameters of the transmission line like R,C,L and Length. We have also made the required connections with the scope so that input and output voltages can be calculated.

Waveforms obtained at the scope block after the completion of simulation.

CONCLUSION

By the study and simulation of Extra High Voltage Transmission lines we have come to the conclusion that they are best suited for transmission of bulk power.

REFERENCES

(1) Circuit Analysis by A.Chakraborthy

(2) IEEE paper by “Karl E. Lonngren and Er-Wei Bai” on “Simulink Simulation of Transmission Line”

(3) MATLAB book (name to be given)

(4) Power System Analysis And Design by B.R.Gupta