SIMULATION OF EXTRA HIGH VOLTAGE LONG
TRANSMISSION LINES
ABSTRACT
The electrical power system mainly consists of three principle divisions
the generating stations, y he transmission system and the distribution system.
The transmission lines are the connecting links between generating station and
the distribution system and lead to other power system interconnections. Now a
day, we are using Extra High Voltage (EHV) transmission lines for transmission of
power between the generating station and distribution system .The main reasons
behind it are the construction of super power stations of very large capacities
necessities the transmission at high voltage for this we use EHV lines.At high
voltages power loss is also reduced because losses are directly proportional to
the square of current. The simulation of transmission line using MATLAB helps
us to analyze the behaviors and parameters of transmission line under actual
conditions. We are simulating a long transmission line and analyze the
waveforms at sending and receiving end. The results obtained after simulation
are used in the designing of Extra High Voltage Long Transmission Line Model.
INTRODUCTION
Electrical energy is generated in large hydro electric, thermal and nuclear
super and super critical power stations these stations are generally situated
far away from the load centers. This necessitates an extensive power supply
network between the generating station and consumer load. This network may be
divided into two parts transmission and distribution the main part of this
transmission system. Transmission line transmits bulk electrical power from
sending end to receiving end stations without supplying any consumer en route
and it can be divided into two parts primary and secondary. The transmission
voltage is re 66kV, 110kV, 132kV, 220kV, 400kV and 765kV.
The more the voltages of transmission line the better the performance and
efficiency of the system. For this we use high voltage and extra high voltage
transmission lines to transmit electrical power from the sending end substations
to the receiving end substations. At the receiving end substations the voltage
is stepped down to a lower value of 66kV, 33kv or 11kV. The secondary
transmission system forms the link between the main receiving end substations
and secondary substations. In the transmission line the voltage can vary as
much as 10% or even 15% DUE TO variation in loads the transmission line is the
main energy corridor in a power system. The performance of a power system is
mainly dependent on the performance of the transmission lines in the system. It
is necessary to calculate the voltage current and power at any point on the
transmission line provided the values at one point are known. We are aware that
in 3 phase circuit problem it is sufficient to compute results in one phase and
subsequently predict results in the other 2 phases by exploiting the three
phase symmetry. Although the lines are not spaces equilaterally and not
transposed the resulting asymmetry is slight and the phases are considered to
be balanced as such transmission line calculations are also carried out on per
phase basis.
The transmission line performance is governed by its four parameters
Series resistance
Series inductance
Shunt capacitance
Shunt conductance
All these parameters are distributed over the length of the line. The
insulation of a line us seldom perfect and leakage currents flow over the
surface of insulators especially during bad weather this leakage is simulated
by shunt conductance. The shunt conductance is in parallel with the system capacitance.
Generally the leakage currents are small and the shunt conductance is ignored
in calculations.
The transmission line may be classified as short, medium and long. When the
length of the line is less than about 80km the effect of shunt capacitance can
be ignored and the line is designated as a short line. When the length is
between 80 and 250km the shunt capacitance can be considered as lumped and the line
is termed as medium length line. Lines more than 250km long require calculation
in terms of distributed parameters are knows as ling lines.
Two Port Networks
A pair of terminals at which a signal (voltage or current) may enter or leave
is called a port. A network having only one such pair of terminals is called a
one port network.
Figure 1. Two-port network
A two-port network (or four-terminal network, or quadripole) is an
electrical circuit or device with two pairs of terminals. Examples include
transistors, filters and matching networks. The analysis of two-port networks
was pioneered in the 1920s by Franz Breisig, a German mathematician.
A two-port network basically consists in isolating either a complete
circuit or part of it and finding its characteristic parameters. Once this is
done, the isolated part of the circuit becomes a "black box" with a
set of distinctive properties, enabling us to abstract away its specific
physical buildup, thus simplifying analysis. Any circuit can be transformed
into a two-port network provided that it does not contain an independent
source.
A two-port network is represented by four external variables: voltage and current
at the input port, and voltage and current at the output port, so that the
two-port network can be treated as a black box modeled by the relationships
between the four variables Vs, Is, Vr and Ir. There exist six different ways to
describe the relationships between these variables, depending on which two of
the four variables are given, while the other two can always be derived.
Note: All voltages and currents below are complex variables and represented
by phasors containing both magnitude and phase angle.
The parameters used in order to describe a two-port network are the
following: Z, Y, A, h and g. They are usually expressed in matrix notation and
they establish relations between the following parameters:
(1)Input voltage V1
(2) Output voltage V2
(3) Input current I1
(4) Output current I2
ABCD Parameters
Figure
2.transmission network
Two port representation of a transmission network.
Consider the power system shown above. In this the sending and receiving
end voltages are denoted by VS and VR respectively. Also the
currents IS and IR are entering and leaving the network
respectively. The sending end voltage and current are then defined in terms of
the ABCD parameters as
So,
This implies that A is the ratio of sending end voltage to the open
circuit receiving end voltage. This quantity is dimension less. Similarly,
i.e., B , given in Ohm, is the ratio of sending end voltage and
short circuit receiving end current. In a similar way we can also define
Also,
The parameter D is dimension less.
Note: Here A and D are dimensionless coefficients, B is
impedance andC is admittance. A negative sign is added to the output
current I2in the model, so that the direction of the current is out-ward,
for easy analysis of a cascade of multiple network models.
SIMULATION
Various blocks used
Resistor
The Resistor block models a linear resistor, described with the following
equation:
Where,
V Voltage
I Current
R Resistance
Connections + and – are conserving electrical ports corresponding to the
positive and negative terminals of the resistor, respectively. By convention,
the voltage across the resistor is given by V(+) – V(–), and the sign of the current
is positive when flowing through the device from the positive to the negative
terminal. This convention ensures that the power absorbed by a resistor is
always positive.
Capacitor
The Capacitor block models a linear capacitor, described with the following
equation:
Where,
I Current
V Voltage
C Capacitance
t Time
Inductor
The Inductor block models a linear inductor, described with the following
equation:
Where,
I Current
V Voltage
L Inductance
t Time
Voltage Sensor
The Voltage Sensor block represents an ideal voltage sensor, that is, a
device that converts voltage measured between two points of an electrical
circuit into a physical signal proportional to the voltage.
Voltage Measurement
The Voltage Measurement block measures the instantaneous voltage between
two electric nodes. The output provides a Simulink signal that can be used by
other Simulink blocks.
AC Voltage Source
The AC Voltage Source block implements an ideal AC voltage source. The
generated voltage is described by the following relationship:
Negative values are allowed for amplitude and phase. A frequency of 0 and
phase equal to 90 degrees specify a DC voltage source. Negative frequency is
not allowed; otherwise the software signals an error, and the block displays a
question mark in the block icon.
Scope
The Scope block displays its input with respect to
simulation time.
The Scope block can have multiple axes (one per port) and all axes have a
common time range with independent y-axes. The Scope block allows you to adjust
the amount of time and the range of input values displayed. You can move and
resize the Scope window and you can modify the Scope's parameter values during the
simulation.
Solver Configuration
Each physical device represented by a connected Simscap block diagram
requires global environment information for simulation. The Solver
Configuration block specifies this global information and provides parameters for
the solver that your model needs before you can begin simulation.
Each topologically distinct Simscape block diagram requires exactly one
Solver Configuration block to be connected to it.
Breaker
The Breaker block implements a circuit breaker where the opening and
closing times can be controlled either from an external Simulink signal
(external control mode), or from an internal control timer (internal control mode).
Ground
The Ground block implements a connection to the ground.
Add
The Add block performs addition or subtraction on its inputs. This block
can add or subtract scalar, vector, or matrix inputs. It can also collapse the
elements of a signal.
Sine Wave
The Sine Wave block provides a sinusoid. The block can operate in either
time-based or sample-based mode.
Fcn Block
The Fcn block applies the specified mathematical expression to its input.
The expression can be made up of one or more of these components:
- u - The input to the block. If u is a vector, u(i) represents the ith element of the vector; u(1) or u alone represents the first element.
- numeric constants
- Arithmetic operators (+ - * /^)
- Relational operators (== != ><>= <=) — The expression returns 1 if the relation is true; otherwise, it returns 0.
- Logical operators (&& || !)-The expression returns 1 if the relation is true; otherwise, it returns 0.
- Parentheses
- Mathematical functions — abs, cos, sin, exp, log, pow, tan, sinh, sqrt etc.
- Workspace variables — Variable names that are not recognized in the preceding list of items are passed to MATLAB for evaluation.
PI Section Line
The PI Section Line block implements a single-phase transmission line with
parameters lumped in PI sections. For a transmission line, the resistance,
inductance, and capacitance are uniformly distributed along the line. An
approximate model of the distributed parameter line is obtained by cascading
several identical PI sections, as shown in the following figure.
Unlike the Distributed Parameter Line block, which has an infinite number
of states, the PI section linear model has a finite number of states that
permit you to compute a linear state-space model. The number of sections to be
used depends on the frequency range to be represented.
PS Simulink Converter
The PS-Simulink Converter block converts a physical signal into a Simulink
output signal. Use this block to connect outputs of a Physical Network diagram
to Simulink scopes or other Simulink blocks.
The Output signal unit parameter lets you specify the desired units for the
output signal. These units must be commensurate with the units of the input
physical signal coming into the block. The Simulink output signal is unitless,
but if you specify a desired output unit, the block applies a gain equal to the
conversion factor before outputting the Simulink signal. For example, if the
input physical signal coming into the block is displacement, in meters, and you
set Output signal unit to mm, the block multiplies the value of the input
signal by 10e3 before outputting it.
Display
The Display block shows the value of its input on its icon. You control the
display format using the Format parameter:
- short - displays a 5-digit scaled value with fixed decimal point
- long - displays a 15-digit scaled value with fixed decimal point
- short_e - displays a 5-digit value with a floating decimal point
- long_e - displays a 16-digit value with a floating decimal point
- bank - displays a value in fixed dollars and cents format (but with no $ or commas)
- hex (Stored Integer) - displays the stored integer value of a fixed-point input in hexadecimal format
- binary (Stored Integer) - displays the stored integer value of a fixed-point input in binary format
- decimal (Stored Integer) - displays the stored integer value of a fixed-point input in decimal format
- octal (Stored Integer) - displays the stored integer value of a fixed-point input in octal format
First Simulation Model
In this we tried to implement the simulation of the transmission line by
using its equivalent diagram.
Figure 3.first simulation model
Although there were no errors but the simulation was not showing desired
results. There was also no consideration of length and solver configuration
block was not implemented correctly.
Second Simulation Model
Consider the standard model1 of a transmission line (Fig. 4).
Figure 4. standard model of transmission line
Both the voltages and the currents can be separately analyzed using Kirchhoff‘s
laws and put in terms that can be analyzed using Simulink. Let’s analyze the
model, writing all time-based variable sin the transmission line in terms of
the Laplace transform variable, s. The spatial variation of the transmission
line will be in corporated into the discrete section number:
For the simulation of the voltage response of the transmission line, the
voltageV1 across the capacitor in the first loop (which includes the voltage
source in Fig.4) can be written in terms of the voltage source, Vs, and the voltage
in the second loop V2 as
Where, Zsis the source impedance. In the transmission
line, the elements L and C are the inductance per unit length, and the
capacitance per unit length, respectively. The voltage across the capacitor in
an Intermediate loop, n, can be written in terms of the similar voltage
Vn-1 in the previous loop (n-l), and the voltage Vn+1 in the following loop
(n+1).
A load impedance, ZL, is in parallel with the capacitor in the final loop,
k. The load impedance can be linear or nonlinear.
We define the current in the load impedance at the end node, k, via
the relation
Where g( Vk) is an arbitrary nonlinear function that has to be
specified by the simulator. In the linear case, g(Vk) is equal to a constant multiplied
by V(Fig. 5). From Fig. 5, we find the voltage Vk to be
Figure 5.simulink simulation of the voltage response of
the transmission line
For purposes of simulating the current response of the transmission line,
the current in the first loop (which includes the voltage source in Fig. 4) can
be written in terms of the voltage source V, and the current in the
second loop i2.
The current in an intermediate loop, n can be written in terms of
the current in the previous loop (n-1) and the following loop (n+1):
For the case of linear load impedance, i =V/ZL, the load
impedance ZL is in parallel with the capacitor in the final loop, k.
The current in this loop is written in terms of the current in the
previous loop (k-1)
Equations 5-7 determine the elements of a second transmission line. In
Fig, 5, the critical Simulink elements are shown for the elements specified
with Equations 1-4. A dialog menu with Simulink allows all parameters of the
polynomial to be specified. We specify the voltage source, Vs, as a half sine
wave generator, which acts as a pulse generator in the simulation. The
amplitude and width were controllable parameters. In our application, fifteen
identical intermediate elements were used. Although we will use only a Limited
number of sections in our transmission line model, it can be generalized to
include as many as desired.
In addition, the user can specify numerical values for the circuit elements
L, C, Zs, and ZL. For clarity of presentation, we
include as equentially increasing “dc offset” to each section. Both linear
[ik=g(Vk) = constant*Vk] and nonlinear [ik=g(Vk)] load impedancesare described
with this model.
Figure 6.matlab simulation model
MATLAB simulation model
But there were two major problems that we were unable to solve First of all
there was no reference to the length of line.
Second the type of function to be used was unknown.
Third Simulation Model
In this we have used a PI Section Line and specifies all the required parameters
of the transmission line like R,C,L and Length. We have also made the required
connections with the scope so that input and output voltages can be calculated.
Waveforms obtained at the scope block after the completion of simulation.
CONCLUSION
By the study and simulation of Extra High Voltage Transmission lines we
have come to the conclusion that they are best suited for transmission of bulk
power.
REFERENCES
(1) Circuit Analysis by A.Chakraborthy
(2) IEEE paper by “Karl E. Lonngren and Er-Wei Bai” on “Simulink
Simulation of Transmission Line”
(3) MATLAB book (name to be given)
(4) Power System Analysis And Design by B.R.Gupta



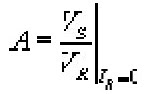



























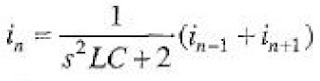




No comments:
Post a Comment